The Klover MiK 09: can a small parabolic microphone outperform a shotgun microphone?

Shotgun microphones (which are typically about a foot long) are used to pick up sounds at ranges of up to several feet, while parabolic microphones (which are typically about two feet in diameter) are used when much longer ranges are required. But why can’t smaller parabolic mics used as an alternative to shotgun mics for shorter-range pick-up? In fact, they can: the MiK 09 and the very similar Sound Shark parabolic reflectors, both by Klover Products, Inc., are intended for just that purpose. In this post I’ll go over the math to show that such a small parabolic microphone is, in fact, an attractive alternative to a shotgun microphone.

How parabolic microphones and shotgun microphones work

Before we get into the details of the Klover MiK 09, it’s probably worth reviewing some basic principles. I have detailed posts on how parabolic microphones work and how shotgun microphones work, but for the purposes of this post, the following summary will suffice:

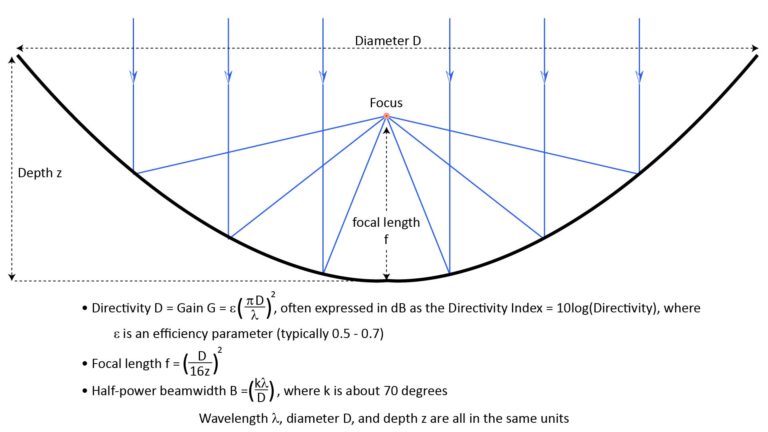
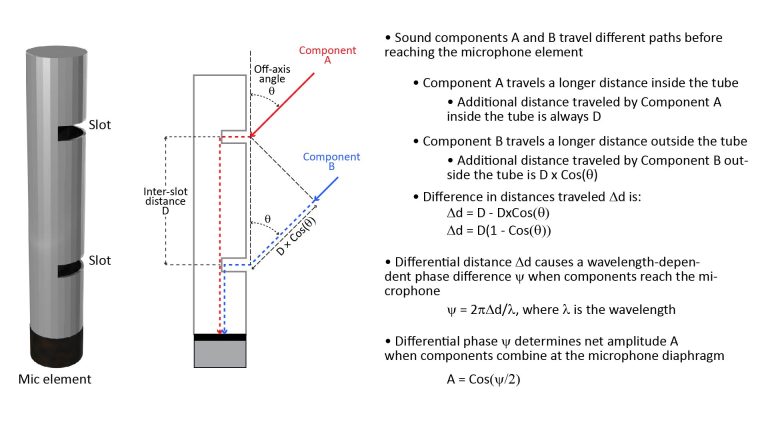
• A parabolic microphone consists of a microphone element mounted at the focus of a parabolic reflector. Sounds arriving along the reflector’s axis of symmetry are captured by the reflector’s mouth and concentrated at the microphone element, but sounds arriving from other directions don’t experience the concentration effect. This makes the microphone directional by amplifying the on-axis sound, and ONLY the on-axis sound.
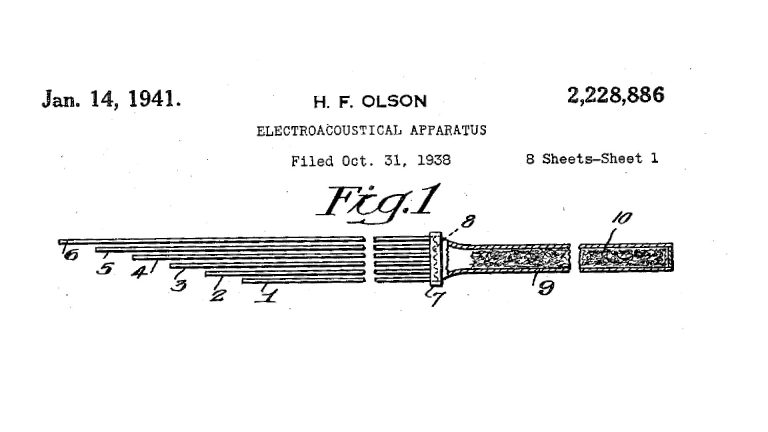
• A basic shotgun microphone consists of a microphone element mounted at one end of a perforated interference tube (there is also a related type of microphone known as a machine-gun microphone, which uses a cluster of tubes instead of a single interference tube). The perforations (or the tubes in a machine-gun microphone) break up incident sound into separate components which recombine at the microphone element. For on-axis sound, the components reach the microphone in-phase, so they recombine constructively. However, for off-axis sound, the components arrive at the microphone element with different phases, whereby they partially cancel through destructive interference. This makes the microphone directional by attenuating the off-axis sound, and ONLY the off-axis sound. Modern shotgun microphones are actually a bit more complex than this because they operate as hypercardioid studio microphones at low frequencies, but we’ll discuss that a bit later in this post.

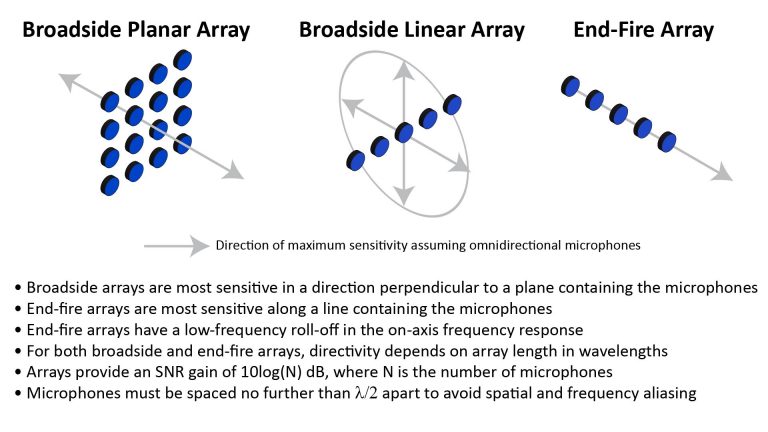
So, while parabolic and shotgun microphones work in different ways, they’re both much more directional than ordinary studio microphones. This characteristic can be quantified by a metric known as directivity, which is the ratio of the microphone’s on-axis response to its average response over all other directions. Directivity can be expressed as a unitless ratio, but is also sometimes expressed in dB as the Directivity Index. Directivity and the Directivity Index are described in more detail in this section of my post on the 4 key microphone specifications.

Directivity is the key to picking-up sounds from long range because it increases the signal-to-noise ratio in the presence of ambient noise, which would otherwise swamp-out the relatively faint on-axis sound. The increase in range due to increased directivity in the presence of isotropic ambient noise is given by the Distance Factor, which is described in more detail in this section of my post on the 4 key microphone specifications.

However, there’s an issue: the directivity provided by parabolic reflectors and shotgun interference tubes (and, in fact, by all high-directivity acoustic devices) depends on their size in wavelengths. This means that practically-sized reflectors and interference tubes provide little directivity at the lower end of the audio spectrum, and also that the variation of directivity with frequency in turn causes the signal-to-noise ratio to vary with frequency. Parabolic reflectors and interference tubes differ in the degree to which they exhibit these effects, as summarized in the following table:

	Parabolic reflector (see how parabolic microphones work for much more detail)	Shotgun microphone interference tube or “machine-gun microphone” tube-cluster (see how shotgun microphones work for much more detail)
Directivity D (unitless)	D≈ε(πd/λ)2, where ε is an efficiency factor that typically ranges from 0.5 to 0.7, d is the dish diameter, and λ is the wavelength	D≈4L/λ, where L is interference tube length (or maximum machine-gun tube length) and λ is the wavelength
Distance Factor DF (unitless)	DF = Sqrt(D) = πd/λ	DF= Sqrt(D) = Sqrt(4L/λ)
Coherent Gain Gc	Gc≈D; in other words, the gain is the same as directivity.	Gc≈1.0
On-axis frequency response	Low-frequency roll-off at 6 dB/octave, per D and Gc	Flat
Beamwidth (-3dB, degrees)	B=kλ/d, where k is 70 degrees, λ is the wavelength, and d is the dish diameter	B=115*sqrt(0.866λ/L), where λ is the wavelength and L is the length of the interference tube

What’s the significance of the gain provided by a parabolic reflector?

Suppose we have a parabolic reflector and a shotgun interference tube that provide the same directivity at a given frequency.

From the previous description of how parabolic reflectors and interference tubes work (and the “coherent gain” row of Table 1), we know that the parabolic reflector works by selectively amplifying on-axis sound, while the interference tube works by selectively attenuating off-axis sound. So, the reflector should provide a greater increase in pick-up range at that frequency, right?

Yes…but the difference might be less than you might expect.

Here’s how gain and directivity affect the signal-to-noise ratio:

• Gain amplifies both the desired sound and the ambient noise, but not the microphone’s self-noise. Thus, gain does nothing to reduce the effects of ambient noise on the signal-to-noise ratio, but it does reduce the impact of microphone self-noise.
• Directivity attenuates the ambient noise level, but not the microphone self-noise.

So, if the ambient noise level is relatively high and the microphone self-noise is relatively low, then the gain provided by a parabolic reflector won’t yield a significant performance benefit. On the other hand, the parabolic reflector’s gain can be a major advantage under low ambient noise conditions, and it can allow the use of a more noisy (and therefore less expensive) microphone element. The only way to know for sure is to do the math, as I describe in my 3-part series on predicting microphone performance (links below).

However, this is a moot question because there is no such thing as a parabolic microphone without gain. What really matters is the actual pick-up range of selected parabolic and shotgun microphones under real-world conditions, and I’ll address that later in this post.

Introducing the Klover MiK 09 Parabolic Microphone by Klover Products, Inc.

Now that we’ve reviewed the basics, let’s introduce the challenger in this virtual face-off: the Klover MiK 09. Klover bills this as a “shotgun killer”–a high-performance alternative to a shotgun microphone.

I’m going to preface this description by stating that I don’t own a Klover MiK 09 (Klover products are highly-regarded, but they’re not inexpensive and I prefer to build my own parabolic microphones). Further, I haven’t actually tested or used a MiK 09, so the performance projections I provide later in this post are based on the equations of Table 1 and the process I describe in my series on predicting microphone performance:

• Predicting microphone performance—Part 1: what is microphone SINR?
• Predicting microphone performance—Part 2: using the SINR
• Predicting microphone performance—Part 3: microphone range prediction

The Klover MiK 09 isn’t a complete parabolic microphone; rather, it’s everything you need to turn an ordinary lavalier (lapel) microphone into a complete parabolic microphone. Here’s a pic of the MiK 09 from the Klover website.

The photos suggest an excellent build quality and level of engineering that are commensurate with the MiK 09’s substantial $375 price. In particular, the cast-aluminum microphone/dish mount is gorgeous.

Specifications

Here are the MiK 09’s specifications, also from the Klover website:

• Range: 30 to 50 feet in ideal conditions
• Amplification: Approximately 6 X
• Dimensions: 10 x 9 x 3 inches
• Dish Outside Diameter: 9 inches
• Collector Diameter: 8 inches
• Weight: Approximately 10 ounces
• Collector Dish Thickness: 1/8 inch
• Frequency: 40 Hz to 15 kHz
• Focus Point: 1-1/8 inch behind the inner face of aluminum frame
• Pickup Pattern: Approximately conical (15 degrees off center) (See “Test Results” tab below)
• Microphone: Omnidirectional lapel up to 5/16 inch diameter
• Mounting Options: Aluminum block with 1/4-20 tapped hole and flash shoe adapter is standard. The block can be replaced with the included cylindrical rod for mounting in a shotgun mic clamp

Of the specifications listed above, four are worth some elaboration:

• The “range” of “30 to 50 feet in ideal conditions”. The useful range of a parabolic microphone depends on so many factors (such as the SPL, spectral distribution, and spatial distribution of both the desired sound and the ambient noise, as well as the required fidelity of the captured sound) that a range specification like this is meaningless. However, a maximum range spec seems obligatory when marketing a parabolic microphone, and 30 to 50 feet certainly isn’t out of the question since even the unaided ear can hear a loud voice at 30 to 50 feet under quiet conditions. So you can’t blame Klover for quoting such a spec. However, as we’ll see, the maximum range in typical applications (such as for videography) will be far less than 30 to 50 feet.
• The “amplification” of “approximately 6 X”. Per Table 1, the on-axis gain of a parabolic reflector depends on the frequency of the sound being captured as well as on the dish efficiency, and Klover quotes neither for the specified “6 X”. Still, as we’ll see, 6 X (which is about 8 dB) is quite a reasonable figure for a dish of this size when used for voice capture.
• The “collector diameter” of 8 inches. This is the effective diameter of the parabolic reflector (the diameter of the surface that actually collects sound), and Klover deserves credit for specifying it in addition to the physical outer diameter of 9 inches. Many parabolic microphone manufacturers specify only one diameter without explicitly stating whether it’s the effective collector diameter or the dish outer diameter (and it’s usually the outer diameter).
• The “Pickup pattern: approximately conical (15 degrees off center)”. Beamwidths are beyond the scope of this post (see how parabolic microphones work for more info), so I’ll just observe that, like gain, the beamwidth of a parabolic microphone is frequency-dependent. And, like Klover’s gain spec, the quoted 30-degree beamwidth is a reasonable figure for a dish of this size when capturing voice.

Microphone mounting and focusing provisions

The photos and video on the website show a microphone mount into which the body of a standard lavalier microphone can be press-fit, and Klover recommends one with an isotropic polar pattern and low self-noise (which makes sense).

An important consideration with any parabolic microphone is that the microphone diaphragm must be accurately positioned at the reflector’s focal point. The photos and assembly video show what appear to be two threaded rods holding the microphone mount, which presumably allow fine adjustment of the diaphragm position during initial assembly of the MiK 09.

However, unlike the threaded adjustment mechanisms in my own DIY parabolic mics, the MiK 09’s mechanism doesn’t allow the focus to be adjusted while the assembled system is in use. This means that the dish can’t be focused by peaking the microphone output level using a test tone, which is how I ensure perfect focus with my own parabolic mics.

Instead, the MiK 09 is focused during assembly by positioning the center of the microphone’s pop filter or grille (which is presumably the location of the diaphragm) at a specified distance from the reflector mounting frame. This isn’t the most accurate way to focus a parabolic microphone, but good results can still be obtained if care is taken in the assembly process.

Now let’s see how the Klover MiK 09 parabolic microphone measures-up against a shotgun microphone.

The Klover MiK 09 versus a typical full-sized shotgun microphone: the Shure VP89L

The shotgun microphone I’m assuming for this comparison is the Shure VP89L.

I analyze the VP89L in my post on how shotgun microphones work, but for the purposes of this post all we need to know about the VP89L is this:

• Like all modern commercially-produced shotgun microphones, the VP89L has a hybrid design that transitions from pure interference-tube operation to hypercardioid operation at frequencies below about 1 kHz.
• The interference tube of the VP89L is about 12 inches long, which is typical of most commercially-available full-sized (versus “shorty”) shotgun microphones.
• The VP89L has a respectably low Equivalent Input Noise (EIN) of just 15 dBA (equivalent to 17 dBZ).

It could be argued that a “shorty” shotgun mic intended for camera-mounting would make for a fairer comparison. However, the MiK 09 is bigger and much more expensive than most camera-mount shotgun mics…and (spoiler alert!) it’s more than a match for the full-length VP89L.

Now that the stage is set, we can compare the projected performance of the Klover MiK 09 and the Shure VP89L using the equations of Table 1.

I’m going to make this comparison in stages: first I’ll discuss how the microphones differ in individual attributes like directivity, gain, and ease of aiming (beamwidth), and then I’ll get to the bottom-line: pickup range.

The Klover MiK 09 parabolic microphone versus the Shure VP89L shotgun microphone: directivity comparison

As I’ve already stated, the most important performance metric of a long-range microphone is directivity, so we’ll begin our comparison with that.

Assumed dish efficiency

As noted in Table 1, the directivity of a parabolic reflector depends partly on an efficiency factor that typically ranges from 0.5 to 0.7. This efficiency, in turn, depends on the accuracy of the dish’s parabolic shape, the smoothness of its inner surface, and the accuracy with which the microphone’s diaphragm is positioned at the dish’s exact focal point.

The MiK 09 appears to have a very high-quality reflector. However, accurately positioning a microphone’s diaphragm at the exact focal point of a dish isn’t easy without actually monitoring the microphone output level during focusing adjustments. The MiK 09 doesn’t allow that.

Therefore, I’m conservatively assuming an efficiency of 0.5 for the directivity and gain estimates in this post, which penalizes the MiK 09 by 1.5 dB relative to an assumed efficiency of 0.7. But as you’ll see, the MiK 09 more than holds its own against the VP89L even with such a conservative efficiency estimate.

Directivity versus frequency

The following figure plots the predicted directivity versus frequency for both the Klover MiK 09 and the Shure VP89L, using the equations of Table 1 and an assumed dish efficiency of 0.5:

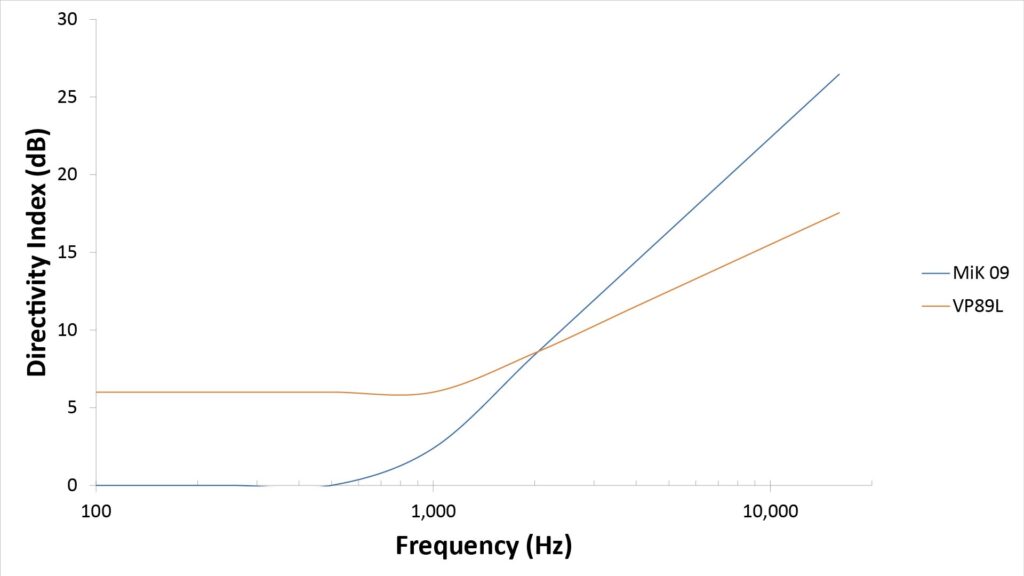
Note that the directivity curve of the VP89L never drops below 6 dB; this is due to the transition to hypercardioid behavior below around 1,000 Hz.

There are three take-aways from these curves:

• Notice that, per the equations of Table 1, the parabolic reflector’s directivity decreases by 6 dB per octave with decreasing frequency, while that of the interference tube decreases by 3 dB per octave with decreasing frequency (until it hits the 6 dB hypercardioid “floor”).
• Interestingly, the directivities cross-over at about 2 kHz—a nice round number that suggests that the MiK 09’s designers might have been targeting a standard-length shotgun microphone as a performance benchmark. Or, it might just be a coincidence, with the MiK 09’s dish diameter having been chosen solely for camera-mounting considerations.
• In any case, the Klover has a significant directivity advantage over the VP89L’s interference tube above 2 kHz, while the VP89L’s low-frequency hypercardioid behavior gives it an advantage below 2 kHz. Since most of the intelligibility of voice is due to frequencies between 1 kHz and 4 kHz, the Klover’s directivity curve would appear to give it an advantage over the VP89, at least for picking-up voice.

Now let’s consider gain.

The Klover MiK 09 parabolic microphone versus the Shure VP89L shotgun microphone: gain comparison

As noted in Table 1, a parabolic reflector has a frequency-dependent on-axis gain equal to its directivity, while a shotgun interference tube has no on-axis gain (or, more precisely, an on-axis gain of 0 dB). Here’s a plot of the gains of the MiK 09 and the VP89L versus frequency:

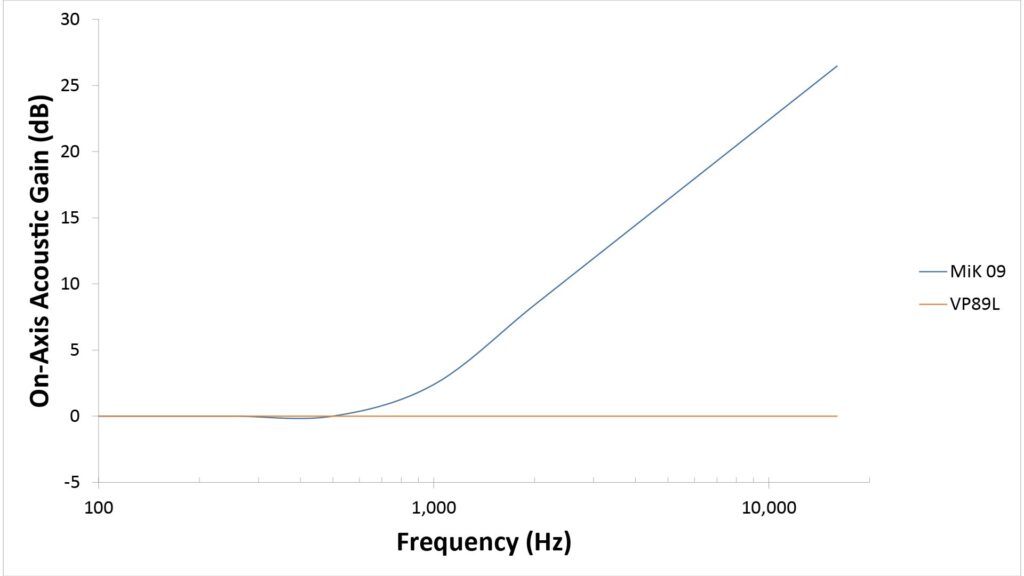
The math actually says that the MiK 09 would provide negative gain below about 760 Hz, but a parabolic reflector can’t actually attenuate low-frequency sound, so the gain never gets below 0 dB. Above 760 Hz, the gain rises at 6 dB per octave, reaching a predicted 26 dB at 16,000 Hz. If we had assumed a perfect 1.0 efficiency instead of 0.5, the gain curve would be 3 dB higher.

An interesting observation to be made from Figure 4 is that the MiK 09’s predicted gain is about 8 dB at 1.9 kHz. That’s significant because the “6 X amplification” quoted by Klover corresponds to 8 dB, and 1.9 kHz is quite a reasonable frequency at which to quote gain, since 2 kHz is the intelligibility peak of the voice spectrum. Klover could easily have based the claimed gain on a higher frequency in order to quote a more impressive number for market purposes. For example, they could have assumed 8 kHz, which would allowed them to quote a gain of 100 X or 20 dB. Klover deserves credit for conservatively basing their gain spec on a frequency that’s much more relevant to voice pick-up.

The significance of the Klover Mik 09’s frequency-dependent gain

As I’ve already explained, frequency-dependent gain is an inherent feature of all parabolic-reflector-based microphones: you can’t have a parabolic reflector’s directivity without gain, and vice-versa.

So, the impact of gain per se on the MiK 09’s performance is of only academic interest. Nevertheless, later in this post I’ll compare the MiK 09’s performance with that of a hypothetical (and impossible-to-achieve) device with the same directivity but no gain.

For now, I’ll just say that the MiK 09’s gain does significantly improve its performance under conditions in which a device like the MiK 09 is likely to be used.

However, there is a more significant implication of a parabolic reflector’s frequency-dependent gain: it results in a non-flat frequency response that requires equalization of the microphone’s output.

Fortunately, the 6-dB-per-octave slope of a parabolic microphone’s on-axis gain, as evident in Figure 4, is extremely easy to equalize. It requires only a first-order filter, which is easy to implement in hardware and even easier to implement using an equalizer plug-in (for livestreaming) or a DAW (for post-processing). Stay tuned for an upcoming post on equalization for parabolic microphones.

The Klover MiK 09 parabolic microphone versus the Shure VP89L shotgun microphone: beamwidth comparison

One of the downsides of a microphone with high directivity is that it reduces the margin for error when aiming toward the source. Since we know that the Klover MiK 09 provides greater directivity than the VP89L above 1 kHz, we know that it will also have less margin for aiming error above 1 kHz. But how much less?

The standard way of characterizing a directional microphone’s sensitivity to aiming error is the beamwidth, which represents the angular width over which the microphone’s sensitivity is within a certain fraction of its peak sensitivity (see post on the 4 key microphone specifications). The most typically quoted beamwidth is the -3 dB beamwidth, which is the angular extent over which the microphone sensitivity is within 3 dB (one-half) of the peak sensitivity.

The following chart shows plots of the -3dB beamwidths versus frequency for both the MiK 09 and the VP89L, using the equations of Table 1. Klover’s pickup-pattern spec of “15 degrees off-center” (or 30 degrees total beamdwidth) is also shown for reference:

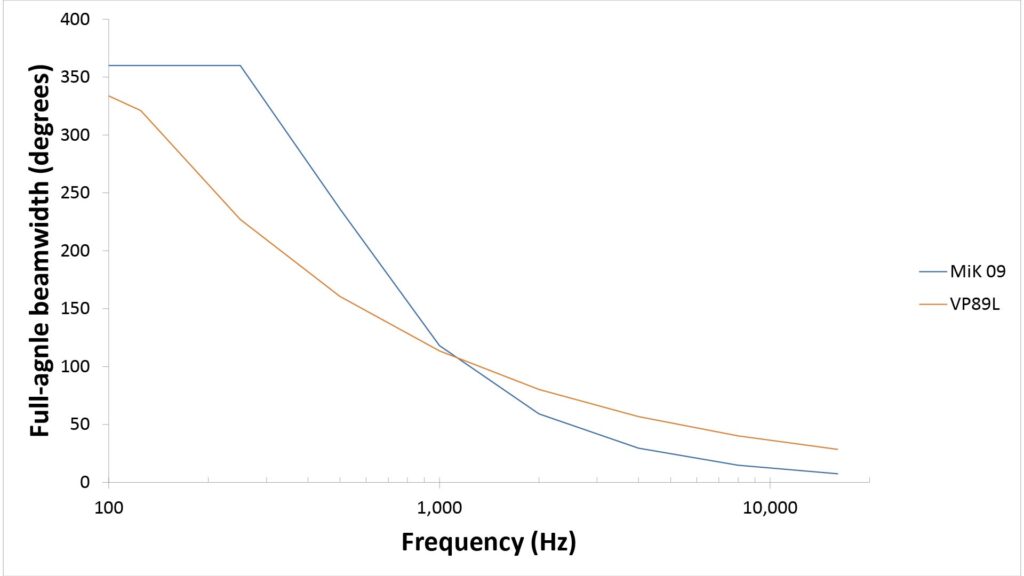
Note that the MiK 09’s predicted beamwidth crosses Klover’s 30-degree spec at about 3900 Hz. That’s not an unreasonable frequency at which to spec the beamwidth for voice. However, for the best vocal fidelity, we’re going to want to capture frequencies up to about 6 kHz (see this section of my post on the key microphone specs for more info)…and at 6 kHz, the MiK 09’s beamwidth is more like 20 degrees (10 degrees off-center), or about the same as the field-of-view of a 100 mm lens on a standard 35-mm camera.

I draw two conclusions from this:

• Klover’s 30-degree “pick-up pattern” spec is reasonable but a little optimistic in terms of the tolerance to aiming error for high-quality voice pick-up.
• Nevertheless, the required 20 degree accuracy at 6 kHz should be easy to achieve in practice.

The Klover MiK 09 parabolic microphone versus the Shure VP89L shotgun microphone: range comparison

Okay, so the MiK 09 has a directivity advantage at higher frequencies but a directivity disadvantage at lower frequencies, and it offers a frequency-dependent on-axis gain which the shotgun mic lacks. But does that make it a “shotgun killer” as claimed by Klover?

The purpose of a shotgun microphone is to be able to capture a desired sound (which is usually voice) at greater ranges than possible with a standard studio microphone. Therefore, we can say that Klover’s claim would be justified if the MiK 09 has a greater range than that of the VP89L when picking-up voice of the desired quality.

It’s because of that last phrase—“of the desired quality”—that microphone range-prediction isn’t as easy as some might think. In this case, we know that the MiK 09 has an advantage over the VP89L at the upper-end of the voice spectrum, but is at a disadvantage at the lower end of the voice spectrum. So how do we make an apples-to-apples comparison of the quality of the output signals over the whole voice bandwidth?

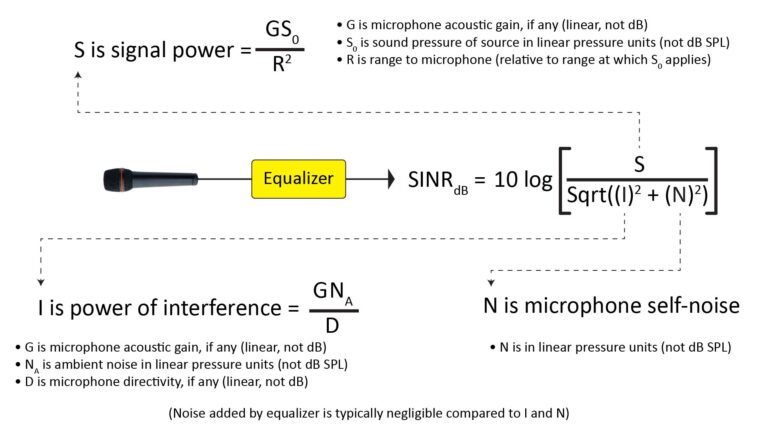
I have a series of post on that very subject (see the references section below for links), but essentially the answer is to use a weighted sum of the Signal-to-Interference-plus Noise Ratios (SINRs) at several frequencies to come up with an “effective SINR” for voice pick-up. We can then use that effective SINR as a basis for predicting the range of microphones that have different SINR-versus-frequency characteristics–and that’s the approach I’ve used for the following range estimates.

Key assumptions

In order to make our SINR-based range comparison, we need to make some assumptions about the sound we’re trying to capture, the ambient noise environment, and the microphone element we’re using with the MiK 09.

Source and ambient noise spectra

I’ve developed reference spectra for voice and ambient noise that are typical of several microphone usage scenarios (see my part 1 of my post on predicting microphone performance for more details).

For this comparison, I’m assuming that we’re trying to pick-up a raised voice (louder than a casual speaking voice but softer than a shout) that has an SPL of 73 dBA measured at 1 foot from the speaker’s mouth. I’m also assuming a relatively quiet ambient noise environment (35 dBA), which is typical of a room that’s somewhat noisier than a recording studio but still fairly quiet. These assumptions are consistent with typical videography applications.

MiK 09 microphone element assumptions

Klover doesn’t recommend any specific lavalier mic for use with the MiK 09, but does suggest that it should have low self-noise.

Most off-the-shelf lavalier mics (even highly regarded ones) actually have a relatively high self-noise. For example, the widely-used Shure MVL (which costs about $65) has an EIN of 29 dBA, while the Countryman B3 (about $240) has an EIN of 24 dBA. However, if you’re willing to do a little soldering, you can build a DIY lavalier microphone with an EIN of just 14 dBA for just $10 in parts.

So, I’m going to include two MiK 09 configurations in this comparison: one with a microphone EIN of 29 dBA, and one with a microphone EIN of 14 dBA.

By the way, Klover also suggests that a microphone element with greater sensitivity will provide greater range. This seems logical, but it simply isn’t true: microphone sensitivity has no impact on the output SINR, which is what determines range. The only practical benefit of using a microphone with high sensitivity is that it allows use of a downstream device (such as a field recorder or DLSR with an external microphone input) that has low sensitivity, but that’s rarely going to be an issue.

Range comparison: fidelity-sensitive applications

The pick-up range of a microphone depends on the minimum acceptable Signal-to-Interference plus Noise Ratio (SINR), which in turn depends on the intended purpose of the captured sound.

I’ve developed two SINR-based quality metrics for microphone range prediction: one for fidelity-sensitive applications (in which good SINR is needed over the whole audio bandwidth), and one for intelligibility-sensitive applications (in which good SINR is needed only over the bandwidth of human speech). These quality metrics are described in detail in part 2 of my series on predicting microphone performance.

Parabolic microphones are often used in applications where fidelity isn’t important, as for surveillance and sports. Fidelity is important, however, for typical shotgun microphone applications–and the MiK 09 is marketed as a high-performance shotgun alternative.

Therefore, for this first comparison, I’m going to plot my signal fidelity metric versus range for four different microphones:

• A high-quality studio microphone with an EIN of 14 dBA and an isotropic polar pattern.
• The Shure VP89L, which has an EIN of 15 dBA.
• The MiK 09 when used with the Shure MVL lavalier mic, which has an EIN of 29 dBA.
• The MiK 09 when used with a DIY lavalier mic with an EIN of 14 dBA.

And here’s how they stack-up:

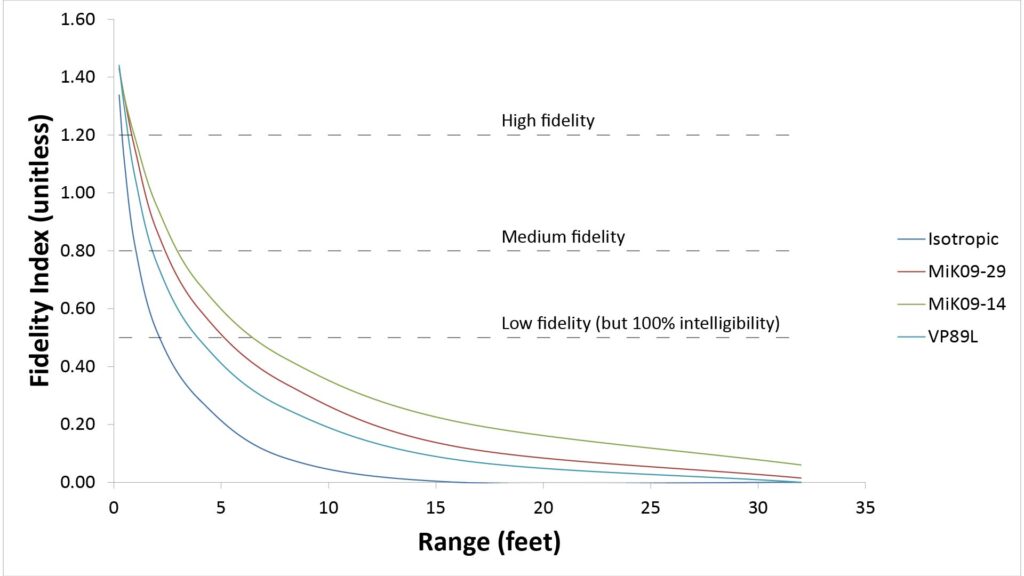
Note that the figure also shows three fidelity thresholds, which I’ve labeled low, medium, and high. For reference, the low-fidelity threshold would typically be considered unacceptable for professional studio microphone applications, but acceptable for many shotgun microphone applications (such as amateur videography). So, that’s the threshold that’s probably most relevant to typical MiK 09 use-cases.

The curves show that the MiK 09 clearly wins this round with the VP89L: it provides noticeably greater pick-up range even with the relatively noisy MVL microphone, and the gap is truly significant when used with a microphone element that’s 10 dB quieter.

However, you might be surprised that the ranges, even for “low” fidelity, are so short. That’s because this fidelity metric includes the SINRs at low frequencies, where the directivity of parabolic and shotgun microphones falls-off.

So, let’s consider an application in which speech intelligibility, but not fidelity, is the driving requirement.

Range comparison: intelligibility-sensitive applications

Since intelligibility doesn’t require as much SINR at low frequencies, the ranges should be significantly greater…and that’s what the math shows:

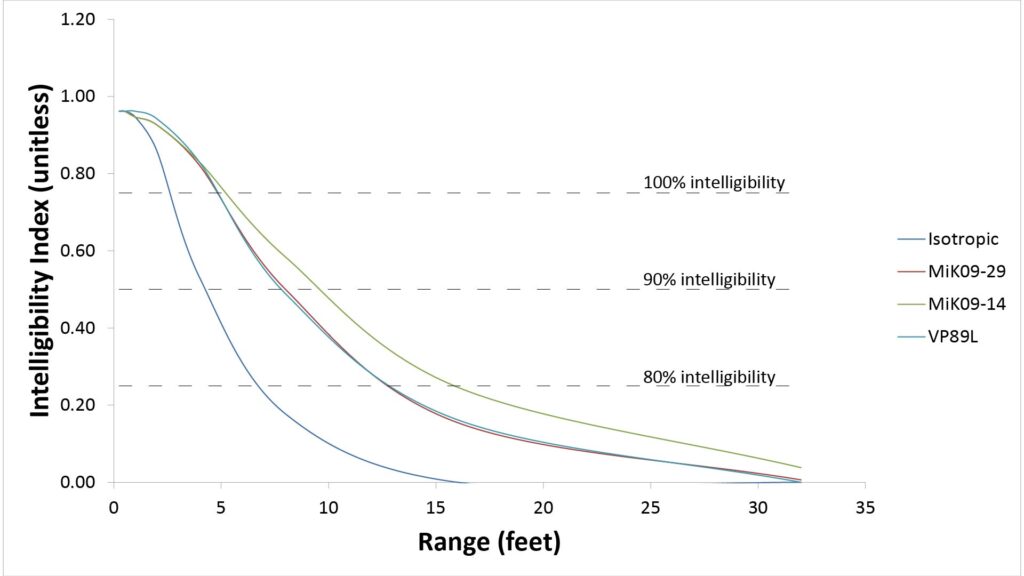
The figure shows three intelligibility thresholds, listed as the percentage of understandable words in whole sentences. The 100% threshold is appropriate for a videography application where high fidelity isn’t critical, while the 80% threshold might be appropriate for a surveillance application.

As we would expect, the ranges are all much greater than those shown in Figure 6. Perhaps surprisingly, however, the MiK 09 provides no range advantage over the VP89L when it’s used with the relatively noisy Shure MVL microphone–but again easily beats the shotgun when used with the quieter mic.

So why was the VP89L able to match the MiK 09/MVL combo in this comparison, but not in the fidelity-oriented comparison? There are two reasons:

• The intelligibility metric used for this comparison doesn’t count any benefit for SINRs greater than 30 dB, whereas the fidelity-oriented metric used in Figure 6 counts benefit for SINRs up to 60 dB. The MiK 09’s SINR exceeds 30 dB at higher frequencies and shorter ranges, so the intelligibility metric doesn’t fully reflect its advantages under those circumstances.
• The VP89L, like all modern shotgun microphones, operates as a hypercardioid microphone at lower frequencies. This gives it a 6 dB directivity advantage over the MiK 09 at those frequencies.

The surprising result shown in Figure 7 is the net result of these factors.

So, if a shotgun can act like a hypercardioid mic at low frequencies, why can’t a parabolic mic do the same thing and reap the same advantages?

Actually, it can!

Range comparison: MiK 09 plus cardioid to enhance low-frequency directivity

While no commercially available parabolic microphones operate this way, it’s certainly possible to use a hypercardioid studio microphone and the parabolic reflector’s isotropic element in parallel, with a cross-over network to rely on the isotropic element at higher frequencies and the hypercardioid microphone element at lower frequencies. In fact, I’ve done that myself, and I’ll post an article on that topic soon.

Let’s see how such a hybrid configuration would perform. But instead of assuming an auxiliary microphone element with a hypercardioid, pattern (which has a directivity index of 6 dB), let’s assume one with a cardioid pattern (which has a directivity index of just 4.8 dB). Despite the 1.2 dB lower directivity, this is a better assumption because microphones with cardioid patterns are more widely available and cost less than those with hypercardioid patterns–especially if you’re into DIY (and you definitely should be).

The following figure shows the result:

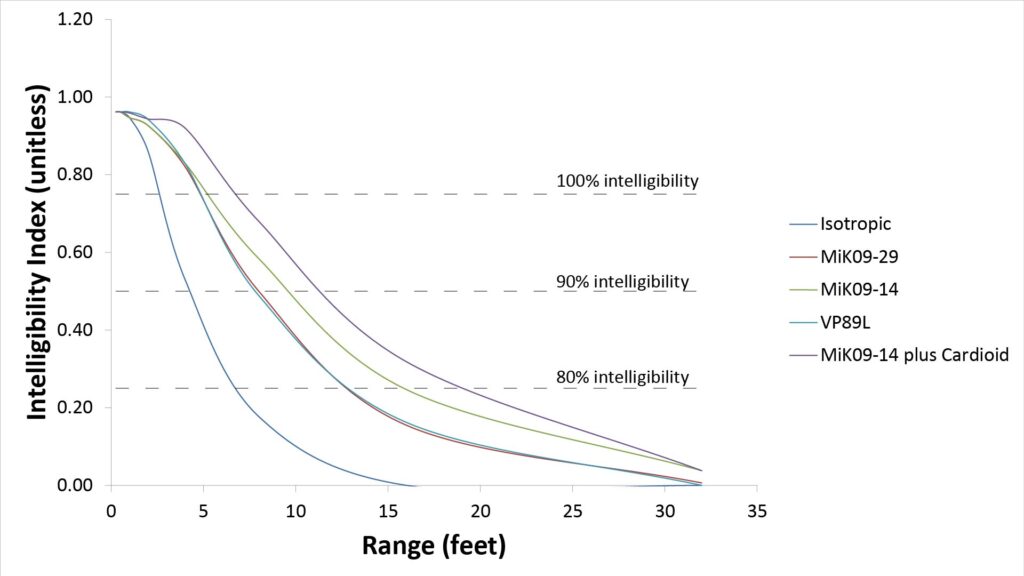
So the hybrid configuration significantly increases the range of the MiK 09 (or the sound quality at a given range). That increased performance is well worth the effort for many applications, especially because it can be achieved at low cost (stay tuned for a post on that).

But how about Klover’s claimed maximum range of 30+ feet?

Before we wrap this up, let’s address Klover’s claim of a maximum range of “30 to 50 feet.” Don’t the curves shown in the preceding figures completely discredit that claim?

In a word, no. There are a lot of variables that determine microphone range, and there are certainly plausible combinations of those variables that could result in a range of 30+ feet. For example, if we assume a quieter ambient noise environment of 25 dBA (typical of a quiet room) and a louder voice (of 76 dBA at 1 foot), we get the following intelligibility-versus-range curve:

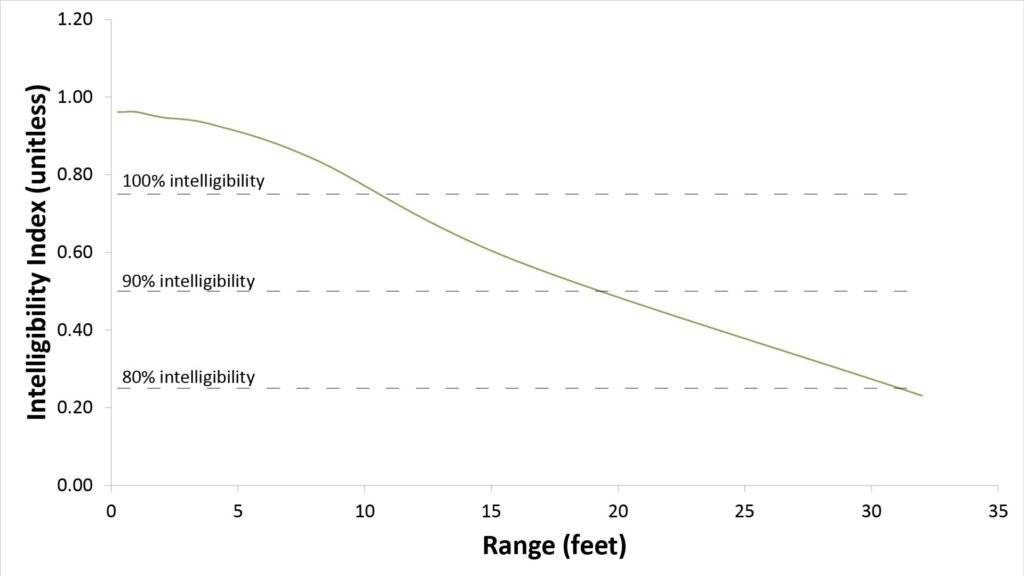
This shows that if we’re willing to accept 80% intelligibility, we can indeed achieve a range of 30 feet under these conditions. Even greater ranges are possible in environments in which the sound isn’t propagating under free-field conditions, but we can’t count on that.

Wrap-up

This little analytical exercise has demonstrated a few things:

• Klover’s claim that the MiK 09 can outperform a typical shotgun microphone isn’t just marketing hype; it’s borne out by the math…and the performance advantage is significant.
• Use of a low-noise microphone (as Klover recommends) definitely makes a difference and is highly recommended.
• The MiK 09’s already-impressive performance can be increased still further by augmenting it with a separate cardioid or hypercardioid studio microphone at low frequencies.
• Klover’s claim of a maximum range of 30 to 50 feet is plausible under ideal conditions, but such conditions are unlikely in typical applications for the MiK 09. Still, this claim doesn’t push the limits of credibility any more than the range claims made by other manufacturers of parabolic microphones. And Klover’s other performance claims are surprisingly consistent with what the math shows; they deserve a lot of credit for truth-in-advertising.

So, while this isn’t a review of the MiK 09, I’d say it’s definitely something to consider if you want a reasonably sized microphone that has a greater pick-up range than a typical shotgun mic.

In fact, if I didn’t build my own microphones and the Klover were less expensive, I might buy one myself.

References

• The math underlying the range predictions in this post is described in my series on microphone performance prediction:
  • Predicting microphone performance—Part 1: what is SINR?
  • Predicting microphone performance—Part 2: using the SINR
• The product page for the MiK 09 by Klover Products, Inc. is at https://www.kloverproducts.com/product/klover-mik-09-parabolic-microphone/
• The product page for the Klover Sound Shark, seemingly functionally identical to the MiK 09 but slightly less expensive, is at https://www.kloverproducts.com/sound-shark/
• The product page for the Shure VP89L is at https://www.shure.com/en-US/products/microphones/vp89